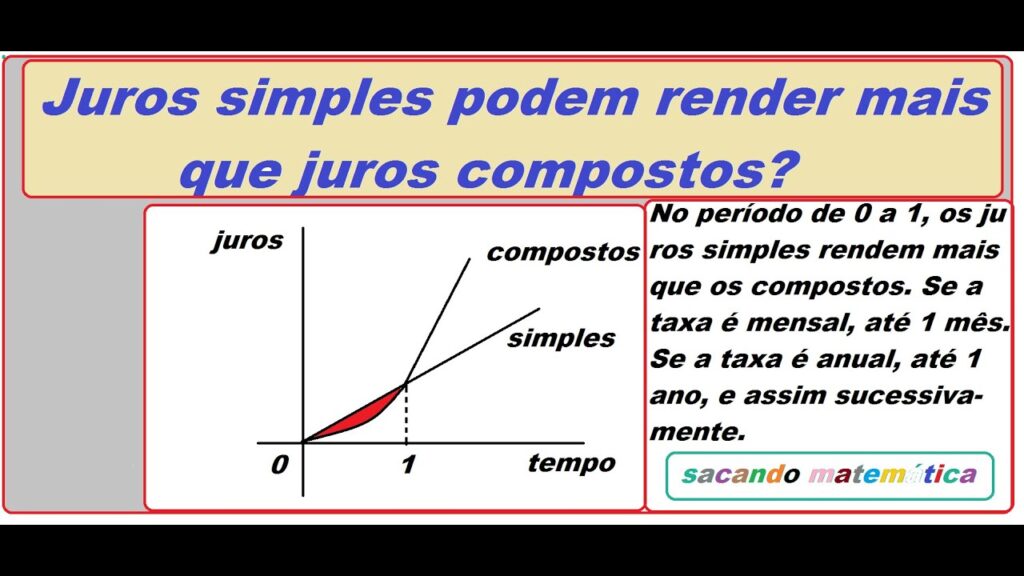
✅ Juro simples cresce linearmente, calculado apenas sobre o valor inicial. Juro composto cresce exponencialmente, calculado sobre o valor inicial e os juros acumulados.
Os conceitos de juro simples e juro composto são fundamentais para a compreensão de como funcionam os investimentos e as dívidas. A principal diferença reside na forma como os juros são calculados. O juro simples é calculado apenas sobre o valor inicial do capital (ou principal) ao longo do tempo, enquanto o juro composto é calculado sobre o capital inicial mais os juros acumulados em períodos anteriores.
O que são juros simples?
Os juros simples são uma forma de cálculo que resulta em um montante que não varia ao longo do tempo, pois é baseado apenas no valor original investido ou emprestado. A fórmula para calcular os juros simples é:
J = C × i × t
- J = juros
- C = capital ou valor inicial
- i = taxa de juros (em decimal)
- t = tempo (em anos)
Por exemplo, se você investir R$ 1.000,00 a uma taxa de 5% ao ano por 3 anos, o cálculo ficaria:
J = 1000 × 0,05 × 3 = R$ 150,00
Assim, ao final do período, o montante total será R$ 1.150,00.
O que são juros compostos?
Os juros compostos, por outro lado, são calculados sobre o capital inicial e também sobre os juros acumulados em períodos anteriores, o que pode resultar em um montante significativamente maior ao longo do tempo. A fórmula para os juros compostos é:
M = C × (1 + i)^t
- M = montante final
- C = capital ou valor inicial
- i = taxa de juros (em decimal)
- t = tempo (em anos)
Usando o mesmo exemplo de um investimento de R$ 1.000,00 a uma taxa de 5% ao ano por 3 anos, o cálculo seria:
M = 1000 × (1 + 0,05)^3 ≈ R$ 1.157,63
A diferença entre os montantes finais é de R$ 7,63, o que demonstra o efeito do juros compostos ao longo do tempo.
Comparação visual entre juros simples e compostos
| Tipo de Juro | Montante Final | Juros Acumulados |
|---|---|---|
| Simples | R$ 1.150,00 | R$ 150,00 |
| Compostos | R$ 1.157,63 | R$ 157,63 |
A diferença entre juros simples e juros compostos não é apenas uma questão de fórmulas, mas também da forma como os investidores e credores devem considerar o tempo e o crescimento de seus investimentos ou dívidas. Ao entender essas diferenças, é possível tomar decisões financeiras mais informadas.
— Como calcular juro simples: exemplos práticos e explicação detalhada
O cálculo de juro simples é um processo bastante direto e fácil de entender. Para calcular os juros simples, utilizamos a seguinte fórmula:
J = C x i x t
Onde:
- J = Montante de juros acumulados
- C = Capital inicial (ou valor principal)
- i = Taxa de juros (em decimal)
- t = Tempo (em anos)
Exemplo 1: Cálculo de juros simples
Vamos considerar um exemplo prático para ilustrar esse cálculo. Suponha que você tenha um capital inicial de R$ 1.000,00, uma taxa de juros de 5% ao ano e um período de 3 anos.
Convertendo a taxa de juros para decimal, temos i = 5/100 = 0,05.
Agora, podemos aplicar a fórmula:
J = 1000 x 0,05 x 3
J = R$ 150,00
Portanto, após 3 anos, o montante de juros acumulados será de R$ 150,00, totalizando R$ 1.150,00 com o capital inicial.
Exemplo 2: Juros sobre diferentes períodos
Vamos complicar um pouco e verificar como o juro simples pode afetar o montante ao longo de diferentes períodos. Imagine que o mesmo capital de R$ 2.000,00 tem uma taxa de juros de 4% ao ano. Vamos calcular o montante de juros para 2, 4 e 5 anos:
| Ano | Juros (R$) | Montante Total (R$) |
|---|---|---|
| 2 | 160,00 | 2.160,00 |
| 4 | 320,00 | 2.320,00 |
| 5 | 400,00 | 2.400,00 |
Como podemos ver, a quantidade de juros aumenta linearmente com o tempo, o que é uma característica fundamental do juro simples.
Vantagens do juro simples
Algumas das vantagens de utilizar o juro simples incluem:
- Facilidade de cálculo: A fórmula é simples e direta, facilitando o entendimento para iniciantes.
- Previsibilidade: Os juros são calculados de maneira constante ao longo do tempo, permitindo um planejamento financeiro mais claro.
É importante lembrar que o juro simples é mais comum em empréstimos de curto prazo e em situações onde a taxa de juros não precisa ser acumulada.
Nos próximos tópicos, discutiremos como o juro composto se diferencia do juro simples e as implicações dessas diferenças nos investimentos e financiamentos.
— Juro composto: entenda o conceito e sua fórmula de cálculo
O juro composto é um conceito financeiro fundamental que se refere à aplicação de juros sobre os juros já acumulados. Isso significa que, diferente do juro simples, onde os juros são calculados apenas sobre o valor principal, no juro composto, o montante cresce de forma exponencial ao longo do tempo.
Como funciona o juro composto?
Para entender o juro composto, é interessante pensar em um exemplo prático. Suponha que você deposite R$ 1.000,00 em uma conta bancária que oferece uma taxa de juros de 5% ao ano. Em um cenário de juro simples, após um ano você terá R$ 1.050,00. Porém, se for em um cenário de juro composto, após o primeiro ano você terá R$ 1.050,00, mas no segundo ano, os juros serão calculados sobre os R$ 1.050,00 e não apenas sobre os R$ 1.000,00 iniciais.
Fórmula do juro composto
A fórmula utilizada para calcular os juros compostos é a seguinte:
A = P (1 + i)^n
- A = Montante final
- P = Capital inicial (valor principal)
- i = Taxa de juros (em decimal)
- n = Número de períodos (anos)
Exemplo prático de cálculo
Vamos aplicar a fórmula acima em um exemplo:
- Capital inicial (P): R$ 1.000,00
- Taxa de juros (i): 5% ou 0,05
- Número de períodos (n): 3 anos
Substituindo na fórmula:
A = 1000 * (1 + 0,05)^3
A = 1000 * (1,157625)
A ≈ R$ 1.157,63
Após três anos, o montante total seria de aproximadamente R$ 1.157,63, demonstrando como o juro composto possibilita um crescimento mais significativo dos investimentos ao longo do tempo.
Benefícios do juro composto
- Crescimento acelerado: À medida que o tempo passa, os juros acumulados aumentam exponencialmente.
- Investimentos de longo prazo: Ideal para quem deseja fazer poupanças ou investimentos duradouros.
- Reinvestimento de juros: Possibilita que os investidores usem os juros ganhos para gerar mais retorno.
Cenário real e estatísticas
De acordo com estudos financeiros, os investimentos em juro composto podem superar investimentos em juro simples em até 10 vezes ao longo de 20 anos, dependendo das taxas. Isso demonstra a importância de uma gestão financeira adequada e a escolha de opções de investimento que proporcionem juros compostos.
Perguntas Frequentes
O que é juro simples?
Juro simples é calculado apenas sobre o valor inicial (capital) durante todo o período.
O que é juro composto?
Juro composto é calculado sobre o capital inicial e também sobre os juros acumulados ao longo do tempo.
Qual é a fórmula do juro simples?
A fórmula é: J = C * i * t, onde J é o juro, C é o capital, i é a taxa de juros e t é o tempo.
Qual é a fórmula do juro composto?
A fórmula é: M = C * (1 + i)^t, onde M é o montante final, C é o capital, i é a taxa de juros e t é o tempo.
Quando usar juro simples ou composto?
Use juro simples em financiamentos de curto prazo e juro composto em investimentos de longo prazo.
Quais são as principais vantagens do juro composto?
O juro composto permite um crescimento exponencial do capital, maximizando os retornos ao longo do tempo.
Pontos-Chave sobre Juro Simples e Composto
- Juro Simples: Calculado apenas sobre o capital inicial.
- Juro Composto: Calculado sobre o capital e os juros acumulados.
- Fórmula Juro Simples: J = C * i * t.
- Fórmula Juro Composto: M = C * (1 + i)^t.
- Uso em Financiamentos: Juro simples é utilizado em empréstimos de curto prazo.
- Uso em Investimentos: Juro composto é mais vantajoso para aplicações a longo prazo.
- Crescimento: Juro composto oferece crescimento exponencial do investimento.
Se você gostou deste conteúdo, deixe seus comentários e confira outros artigos do nosso site que podem ser do seu interesse!